Ruffini, autor de una regla de dudosa aplicación
- ALEXÁNDER GRANADA RESTREPO

- 3 abr 2024
- 4 Min. de lectura

Envía esta noticia: ALEXÁNDER GRANADA RESTREPO, "MATU SALEM"*
Seguimos con una de las grandes hazañas matemáticas, que implicó durante siglos a muchas de las grandes mentes de la ciencia: la resolución de las ecuaciones polinómicas. El gran matemático italiano Paolo Ruffini (1765-1822) también tuvo su protagonismo en la resolución de las ecuaciones de 5º grado. Le dedicamos la siguiente entrada, dentro del especial del Año de la Cristalografía.
Paolo Ruffini fue un matemático italiano, que vivió del 1765 al 1822. Muchas personas le recordarán del colegio, por su contribución más famosa: el llamado método de Ruffini, que permite hallar los coeficientes del polinomio que resulta de la división de un polinomio cualquiera por un binomio del tipo (x-a). Aunque sin duda su mayor contribución al desarrollo de la matemática fue la demostración de la imposibilidad de la solución general de las ecuaciones algebraicas de grados quinto y superiores.
Demostró, alrededor del 1800, que la ecuación general de quinto grado no se podía resolver con una fórmula en la que solo aparezcan operaciones elementales, es decir, sumar, restar, multiplicar, dividir y calcular raíces cuadradas.
Hasta este grado, con las ecuaciones de hasta cuarto grado, sí se había podido hacer. Los matemáticos tardaron varios siglos en completar la hazaña, pero ya se conocían las fórmulas para la resolución de la ecuación general de 4, 3 y 2 grado. Sin embargo, Ruffini afirmaba que, a partir de las de 5º, el planteamiento es otro: no se podía, por mucho que es intentara, dar con esta fórmula, y el trabajo de todos los que la habían codiciado hasta entonces, fue inútil.
Ruffini publicó en 1799 sus resultados en una obra de dos volúmenes llamado “Teoría general de las ecuaciones”. El resultado era de importancia capital, porque zanjaba el tema de la búsqueda general de la forma, aunque fuese de manera negativa. Sin embargo, sus coetáneos no lo supieron asimilar: la demostración era tremendamente complicada y el razonamiento casi imposible de seguir. Nadie hizo caso de este avance.
Ruffini le mandó el escrito a Lagrange en tres ocasiones, la primera en 1801, pero no le contestó en ninguna de ellas. También probó a publicar otras versiones más sencillas, discutió el resultado con algunos de sus colegas… pero tampoco consiguió hacer trascender sus resultados. Fue como si el resultado no existiera. Evidentemente, también en la ciencia, si cae un árbol en medio del bosque y no lo oye nadie, es como si no cayera. En este caso, además, nadie quería prestar atención pues cualquier decisión de sus pares, ya fuese para validar o invalidar su prueba, requería de un ingente esfuerzo (para comprender la prueba), que grandes matemáticos, de la talla de Lagrange, no estaban dispuestos a invertir.
Las bases de la revolución del
álgebra hacia la teoría de grupos

Portada de la Teoría general
de la ecuación (1799)
En un último intento, Ruffini mandó la prueba a la Royal Society de Londres –que contestaron diciendo que ellos no hacían validaciones públicas de demostraciones- y a Cauchy. Éste último fue el único matemático que hizo una apreciación positiva del trabajo, en una carta que mandó al propio Ruffini seis meses antes de su muerte. Pero ni con esas se difundió el trabajo de Ruffini.
Hay que decir que, incluso en la actualidad la mayoría de los matemáticos no son capaces de establecer la verosimilitud de la prueba, debido a su complicación. Puede decirse que no demostró del todo que la ecuación de quinto grado no se podía resolver mediante una fórmula compuesta por operaciones simples. En su escrito hay una laguna importante, en la que Ruffini daba por sentado algo que no era evidente, sino que era necesario comprobar. Pese a ello, su trabajo era innovador y revolucionario. Cambió el planteamiento de la investigación: no había que buscar la fórmula, sino que demostrar que no la había.
Además, sus escritos contenían ideas fundamentales en la transición del álgebra tradicional (que trataba únicamente de números) a la teoría de grupos (que trata de elementos y operaciones entre ellos). Sentó las bases del trabajo revolucionario que luego harían dos de los grandes héroes de la historia de las matemáticas: Niels Henrik Abel y Evariste Galoise, de los que hablaremos en futuras entradas.
Médico y matemático

Universidad de Módena, donde fue designado rector.
Ruffini fue consciente de su fracaso, en el campo de las matemáticas, y siguió ejerciendo como médico. No lo hemos dicho, pero esta era su profesión paralela. Siguió la carrera de su padre, Basilio Ruffini, que era médico en Valentano. Antes de eso, de niño parecía destinado a la carrera religiosa. Pero al entrar en la universidad de Módena en 1783 para estudiar matemáticas, medicina, filosofía y literatura.
Aprendió cálculo y geometría, y en particular estudió los fundamentos del análisis. En 1788, fue nombrado profesor de fundamentos de análisis, y poco después, fue elegido catedrático de Elementos de Matemáticas en 1791. También, en 1791, obtuvo la licencia para ejercer la medicina en Módena.
Explicación
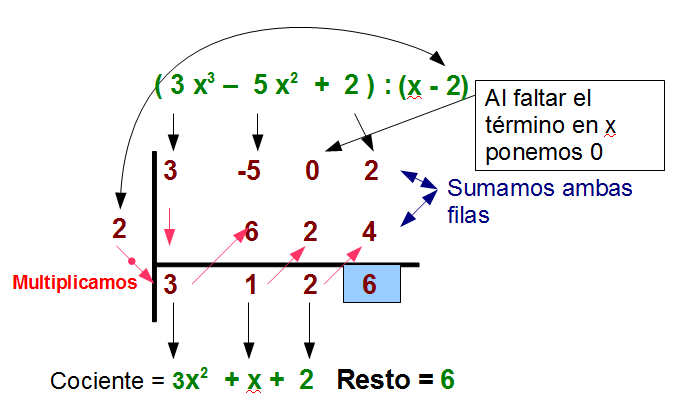
En la clase de hoy te explicamos la Regla de Ruffini con teoría y ejemplos.
En ocasiones al dividir polinomios nos podemos encontrar con un divisor de primer grado de la forma x-a :
Veamos el siguiente ejemplo,
Siendo:
P(x)= 3x3+13x2-13x+2
V(x)= x-1
Realizar la siguiente operación:
(3x3+13x2-13x+2): (x-1)=
Así: C(x)=3x2+16x+3 y R(x)=5
En este sentido, Paolo Ruffini (1765-1822), matemático y médico italiano, estableció un método que se conocería como Regla de Ruffini para realizar este tipo de operaciones. No obstante, hizo otras aportaciones importantes para las matemáticas. De hecho, fue el primero en demostrar que la ecuación de quinto grado no se podía resolver por radicales.A continuación vamos a realizar los pasos que debemos seguir para realizar la división hecha anteriormente, pero esta vez aplicando el método de Ruffini:
(3x3+13x2-13x+2): (x-1)=
En primer lugar colocamos los coeficientes del dividendo en un fila. En este caso el polinomio es completo, si no fuera así completaría con ceros, 0.
(3x3+13x2-13x+2): (x-1)=
Posteriormente, colocamos el opuesto (le cambiamos el signo) del termino independiente del divisor.
(3x3+13x2-13x+2): (x–1)=
Para empezar, bajamos el primer coeficiente.
Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
Sumamos los dos coeficientes.
Repetimos el proceso anterior y vamos completando paso a paso la tabla.
Aquí, debemos tener en cuenta que:
El grado del cociente es una unidad inferior al grado del dividendo.
El resto es siempre un número.
Así: C(x)=3x2+16x+3 y R(x)=5
Fuente: madrimasd.org / 20 MINUTOS

*Escritor, poeta teórico y filósofo. Autor de "Las caravanas de Matusalém".





Comentarios